The Monad of FP
Applicative 无法解决的问题
通过 Applicative,我们可以将值为 unary 参数的函数的 Functor 与另一个 Functor 进行组合,但如果值的类型是 Type Class 的话,比如 Option,Applicative 也无能为力了,比如:
import { Option, some, none, option } from "fp-ts/Option";
import { head } from "fp-ts/Array";
const inverse = (n: number): Option<number> => (n === 0 ? none : some(1 / n));
const inverseHead: Option<Option<number>> = option.map(
head([1, 2, 3]),
inverse
);
注意这里的inverseHead的类型变成了Option<Option<number>>,但我们期望的结果应当是Option<number。
在实际开发中,如果这个 Type Class 是数组的话,问题很容易就解决了,因为我们可以利用Array.prototype.flat方法将数组偏平化,如下:
const arr1 = [0, 1, 2, [3, 4]];
console.log(arr1.flat());
// [0, 1, 2, 3, 4]
如果 Option 也有相应的flat方法的话,那问题不就迎刃而解了吗?而 Monad 就是拥有这种能力的 Type Class。
Chain
介绍 Monad 之前,我们需要先了解另外一个 Type Class,Chain,它的定义如下:
export interface Chain<F> extends Apply<F> {
readonly chain: <A, B>(fa: HKT<F, A>, f: (a: A) => HKT<F, B>) => HKT<F, B>;
}
可以发现,它继承于 Apply,同时额外添加了chain方法,该方法的语义等同于数组的flat方法,即将 Type Class 扁平化。
对于文章开头的例子,可以改写为:
import { Option, some, none, option } from "fp-ts/Option";
import { head } from "fp-ts/Array";
const inverse = (n: number): Option<number> => (n === 0 ? none : some(1 / n));
// 使用 option.chain 而不是 option.map
const inverseHead: Option<number> = option.chain(head([1, 2, 3]), inverse);
由于chain方法和flat在语义上一致,因此有时候它的别名也叫作flatMap,而且后者往往更常见,可能是因为它包含flat这个前缀,因此语义性更强。
除此之外,一个 Type Class 是否是 Chain,要求它的chain方法满足关联性(Associativity),如下:
F.chain(F.chain(fa, afb), bfc) <-> F.chain(fa, a => F.chain(afb(a), bfc))
Monad
熟悉 Chain 之后,我们再来看 Monad 的定义,如下:
export interface Monad<F> extends Applicative<F>, Chain<F> {}
可以发现,Monad 同时继承于 Applicative 和 Chain,但没有提供任何额外方法,因此将这两个 Type Class 组合起来,就是 Monad 在 Type Class 上的类型定义。
除了类型定义之外,Monad 还要额外满足 3 个约束,如下:
- 左恒等性:
flatMap(of) ∘ f = f - 右恒等性:
flatMap(f) ∘ of = f - 关联性:
flatMap(h) ∘ (flatMap(g) ∘ f) = flatMap((flatMap(h) ∘ g)) ∘ f
Monad in Category
在范畴论中,Monad 实际上是 Kleisli 三元组中的一个概念,而另外两个概念分别是一个范畴(Category) 和一个映射(Morphisms),映射有时候也被称作 Kleisli Arrow,描述的是这样一种逻辑,如下图:
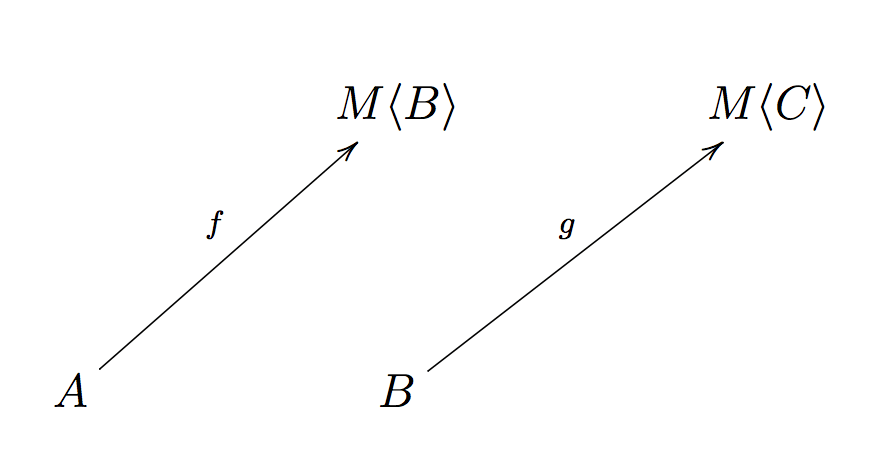
范畴论是研究 Composition 的学科,因此,我们是否可以找到 A => M<C> 的映射关系呢?或者说,这两个 Kleisli Arrow 的组合,如下图:
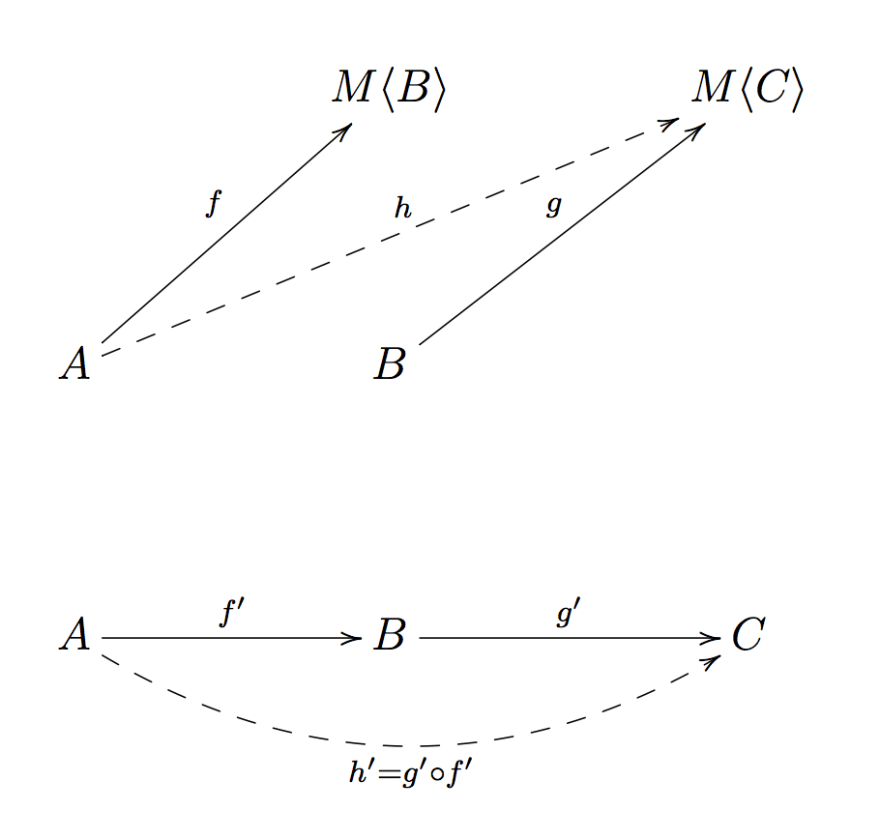
上图中的下半部分不用证明,因为这就是之前介绍 Category 概念时的那张图的另外一种画法,我们要找的 A => M<C> 的映射关系,即是上半部分中的 h。
在这里我们可以利用范畴论中的逻辑来找到 h,因为当前已经存在一个 A => M<B> 的映射 f,那么我们只要找到 M<B> => M<C> 的映射(假如叫作 k)的话,h 不就等价于 k ∘ f 吗?
如何找到 k 呢,大概可以按下图这样:
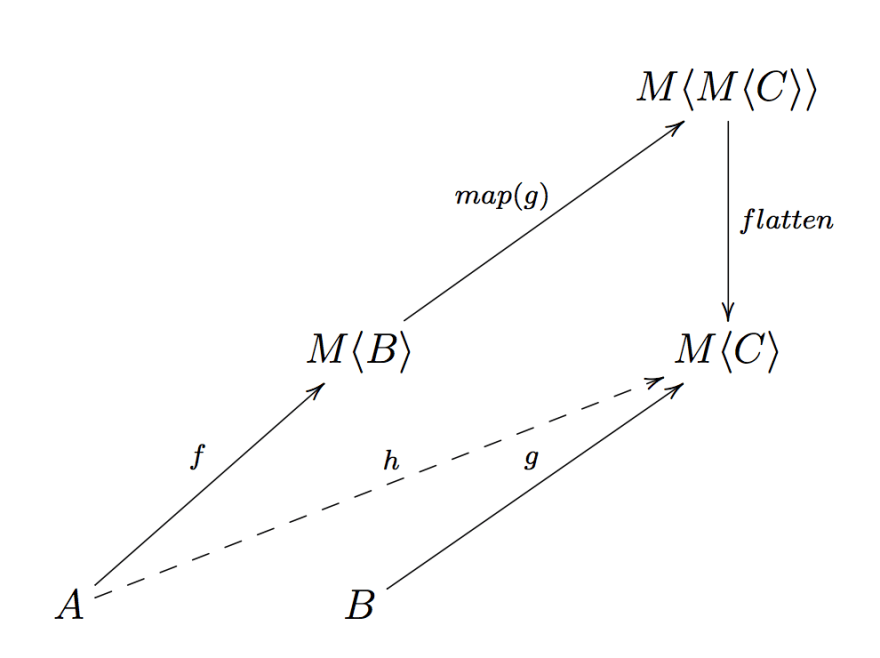
对于map(g)的部分,实际上它就是 Functor 要解决的问题,即M<B>.map(g),之后我们可以得到 M<M<C>>。而对于flatten的部分,实际上它就是 Chain 要解决的问题,即扁平化 Type Class,使M<M<C>>变成M<C>。
由于我们找到了 M<B> 到 M<C> 的映射关系 k,即k = flatten ∘ map(g),随后又可以推导出h = flatten ∘ map(g) ∘ f。
由于范畴论中约定对象之间的映射要满足关联性,因此我们可以把flatten ∘ map(g)组合起来并替换成一个更具语义的名字,即flatMap(g),最终得到h = flatMap(g) ∘ f。
最后,范畴论同时要求对象始终拥有一个指向自身的映射,即满足恒等性,如下图:
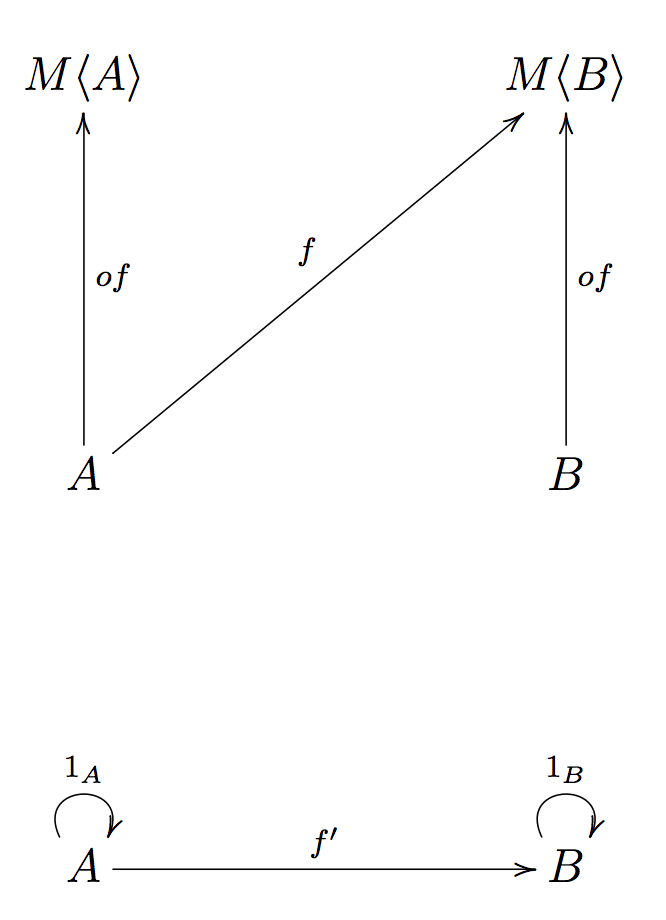
为什么 Monad 要满足约束
在 Monad in Category 中,我们将函数式编程的问题,转化为了范畴论中的问题,并最终找到了 A => M<C> 的映射关系,但映射关系成立的前提,是这些对象在一个范畴当中,而一个范畴,要满足范畴论中的所有约束。
因此 Monad 在函数式编程中,要遵守的约束条件,本身就代表范畴论中那些约束条件,只是编程语言场景下的不同表现形式罢了,这里用表格做一个归纳,如下:
| Law | K | TS |
|---|---|---|
| Left identity | 1B ∘ f' = f' | flatMap(of) ∘ f = f |
| Right identity | f'∘ 1A = f' | flatMap(f) ∘ of = f |
| Associativity | h' ∘ (g' ∘ f') = (h' ∘ g') ∘ f' | flatMap(h) ∘ (flatMap(g) ∘ f) = flatMap((flatMap(h) ∘ g)) ∘ f |
Promise 是否是 Monad
要证明 Promise 是否是 Monad,只要挨个验证 Promise 是否满足 3 条约束即可,如下:
// 对于 Promise 来说,flagMap 实际上就是实例对象的 then 方法
// 而 of 实际上就是 Promise 对象的 resolve 静态方法
// 左恒等性验证
const value = 42;
const f = (x) => Promise.resolve(x + 1);
Promise.resolve(value).then(f); // Promise { 43 }
f(value); // Promise { 43 }
// 右恒等性验证
const promise = Promise.resolve(value);
promise.then((x) => x); // Promise { 42 }
promise; // Promise { 42 }
// 关联性验证
const g = (x) => Promise.resolve(x * 2);
const h = (x) => Promise.resolve(x - 1);
promise.then(f).then(g).then(h); // Promise { 85 }
promise.then((x) => f(x).then(g)).then(h); // Promise { 85 }
表面看,似乎 3 条约束都满足,但 Promise 实际上不是 Monad,原因如下:
// 第一,Promise.resolve 和 of 很像,但它同时也实现了 flatMap 的逻辑
Promise.resolve(Promise.resolve(1)); // Promsie { 1 }
// 符合期望的返回结果应该为 Promise { Promise { 1 } }
// 第二,对于有 .then 方法的对象,Promise.resolve 也会将它扁平化,如下:
Promise.resolve({ then: (x) => x(2) }); // Promise { 2 }
// 因此,在特殊情况下,会发生异常,如下:
const obj = { then: (x) => x(2) };
const f = (x) => Promise.resolve(x.then);
f(obj).then((res) => console.log(res)); // 会打印结果 x => x(2)
Promise.resolve(obj)
.then(f)
.then((res) => console.log(res)); // 会打印结果 undefined
上面例子中具有.then属性的对象,在 js 中被称作 thenable,同时这里也引用 MDN 关于 Promise.resolve 在调用时,如何解析返回值的描述:
The Promise.resolve() static method “resolves” a given value to a Promise. If the value is a promise, that promise is returned; if the value is a thenable, Promise.resolve() will call the then() method with two callbacks it prepared; otherwise the returned promise will be fulfilled with the value.
Rxjs 中的 Observable 是否是 Monad
这里直接给出答案,是的,Observable 是 Monad,证明的过程就不赘述了,有兴趣的可以自行证明。
Promise 的替代品
即然 Promise 不是严格遵循函数式编程的异步解决方案,有没有其他解决方案呢?答案是有的,即 Task。
Task 这个 Type Class 的语义表示永远不会失败的异步任务,对于可能失败的异步任务,可以使用 TaskOption 或 TaskEither,它们都是 Monad 的实例。
关于它们的介绍不在这篇文章中展开,会在之后的文章中介绍。