The Functor of FP
Category 与范畴论
范畴(Category),是函数式编程中非常重要的一个概念,虽然题目是关于函子(Functor)的,但要介绍 Functor 就不得不先介绍 Category。
简单说,Category 可以理解为一个包含若干对象(Objects)以及它们之间的映射关系(Morphisms)的集合,如下图:
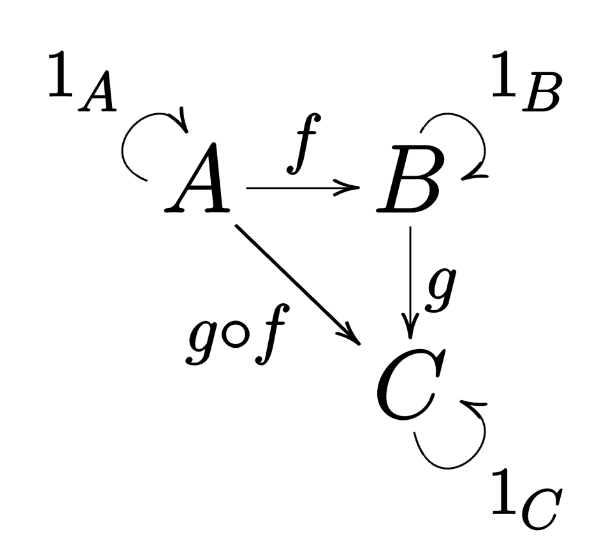
图中的箭头表示映射关系,因此我们可以得出如下结论:
- 由
f: A => B和g: B => C可得g ∘ f: A => C(可组合性) - 如果
f: A => B,g: B => C并且h: C => D,则h ∘ (g ∘ f)和(h ∘ g) ∘ f等价(关联性或结合性) - 每个对象都一个
identify: A => A的映射关系(恒等性)
只看上面这种图,实际上和函数式编程还没什么关系,因为它只是范畴论(一个数学学科分支)中经常用来介绍 Category 的一张插图,但是,数学中最重要的抽象,因此上图中的 Objects 和 Morphisms 都可以替代成任何概念,只要它满足可组合性、结合性和恒等性,我们就可以称它是一个 Category。恰巧,这件事儿在上世纪 50 年代就已经被美国数学家 William Lawvere 和 Saunders Mac Lane 提出并证明了。
具体来说,Moggi 在他的论文《计算 lambda 演算中的范畴 Semantics》中提出了将 Haskell 类型系统的概念与范畴论进行对应的想法。这样做的目的是为了让计算机科学家在应用函数式编程时能够更好地理解范畴论。
而后,Wadler 在他的论文《Monads for functional programming》中进一步完善了这个想法,提出了将 Haskell 中的 monad 概念与范畴论中的模变换(Functor)、自然变换(Natural Transformation)和单子范畴(Monad Category)等概念对应的想法。他证明了一个重要定理,即所有的 Monad 都可以用范畴论中的三个概念来表示和解释。
换言之,我们可以利用范畴论这门强大的数学工具来解决编程中遇到的实际问题,因为它们彼此在概念上是等价的,这就是函数式编程。
Category 与函数式编程
因此,我们在函数式编程中,可以找到与范畴论中与 Category 等价替换的概念,如下:
- Objects: 即代码中声明的数据类型(Types),如 string, number, Array<string> 等
- Morphisms: 即处理数据的函数(Function),如
(a: string) => boolean ∘: 实际上就是compose方法的实现,只要函数在编程语言中是一等公民(如 javascript)就可以很容易地实现该方法
上文中的那张插图,可以等价用代码实现,如下:
// A 表示 string
// B 表示 number
// C 表示 boolean
function f(s: string): number {
return s.length;
}
function g(n: number): boolean {
return n > 2;
}
function h(b: boolean): number {
return b ? 1 : 0;
}
// k = g ∘ f
function k(s: string): boolean {
return g(f(s));
}
// p = h ∘ g
function p(n: number): number {
return h(g(n));
}
// 满足可组合性
// g ∘ f: string => boolean 和 k: string => boolean 等价
g(f("foo")) === k("foo");
// 满足结合性
// h ∘ (g ∘ f) 和 (h ∘ g) ∘ f 等价
h(k("foo")) === p(f("foo"));
对于identity: A => A的实现也非常简单,如下:
function identity<A>(a: A): A {
return a;
}
// 满足恒等性
identity("foo") === "foo";
有上面例子可知,f和g是可组合的,原因是因为f的返回值类型正好和g的参数类型一致(对于g和h也同理),而f和h却是不可组合的。
但有没有一种可能,我们可以把f和h也组合起来调用呢?答案当然是可以的,这就轮到今天的主角 Functor 登场了。
Functor come to rescue
为了解决上文提及的f和h不可组合的问题,需要引入 Functor 的定义,这里为了方便解释,暂时先不把范畴论的定义搬过来,而是采用函数式编程中的关于 Functor 类型的定义。
Functor 的类型签名通常写作(F, map)或者用 typescript 中 interface 的声明可写作(这里引用fp-ts库的声明):
// 假设 F 是一个一元构造函数, 表示 any => F<any>
export interface Functor<A> {
readonly map: (fa: Functor<A>, f: (a: A) => B) => Functor<B>;
}
// 有时候 map 也会被写作 lift,函数签名会发生变化,但本质是一样的
export interface Functor<A> {
readonly lift: (f: (a: A) => B) => (fa: Functor<A>) => Functor<B>;
}
map和lift的本质是一样的,只是参数的顺序不一样,其最终的函数返回类型均是F<B>。
重点来了,Functor 必须要满足以下两个条件(这是 Functor 在范畴论中定义要具备的特性):
lift(identity<T>)要与identity<F<T>>等价lift(g ∘ f)要与lift(g) ∘ lift(f)等价
在语义上,map和lift分别从两个不同的角度,来描述“映射”这件事儿:
map:更着重针对F,表示能够把F<A>映射为F<B>lift:更着重针对“映射“所对应的函数,表示把该映射逻辑,提升(lift单词的语义)至某个上下文(指F)中
对于f和h不可组合的问题,我们可以重新定义number和boolean类型(使用 Functor 的概念,使它们满足某种约定,即上面所提及的两个条件)。
在 js 中,我们可以很容易地使用Array作为抽象Functor的方式,如下:
type ArrayFunctor<T> = Array<T>;
// 使用 Array 作为容器的 F 构造函数的实现
function F<T>(t: T): ArrayFunctor<T> {
return [t];
}
之后重新实现f和h函数,如下:
function f(fs: ArrayFunctor<string>): ArrayFunctor<number> {
return fs.map((s) => s.length);
}
function h(fb: ArrayFunctor<boolean>): ArrayFunctor<number> {
return fs.map((b) => (b ? 1 : 0));
}
这时,f和h就具备了可组合性。
但值得注意的是,这里的可组合性指f和h本身,而原先函数中的代码,只是以映射的方式,被包含在Functor这个上下文中,并通过map方法调用,如果只看映射逻辑函数本身,仍然是不可组合的(因为类型前后不一致),但这却带来了很多便利性和优势。
在实际生产中,f和h可能代表两个非常复杂的组件,要适配这两个复杂组件的常用解决方案就是引入一个中间件来适配它们,如下:
function f(s: string): number {
return s.length;
}
function h(b: boolean): number {
return b ? 1 : 0;
}
// 编写一个中间件函数 m 适配 f 和 h
function m(a: number): boolean {
return Boolean(a);
}
h(m(f("foo")));
或者压根就不存在f或者g函数,它们是以代码块而存在的,这时就会直接在函数中直接增加额外的代码来完成中间件的适配逻辑,比如:
function app(s: string): boolean {
// the logic of f
const fr = s.length;
// the logic of m
const mr = Boolean(fr);
// the logic of h
return mr ? 1 : 0;
}
随着时间的推移,潜在的m会不断出现(因为需求总在变更,或者程序有 bug),这时你的代码中会出现m1,m2和m3(甚至更多)。
但如果采用 Functor 的写法,则会是这样:
function f(fs: ArrayFunctor<string>): ArrayFunctor<number> {
return fs.map((s) => s.length);
}
function h(fb: ArrayFunctor<boolean>): ArrayFunctor<number> {
return fs.map((b) => (b ? 1 : 0));
}
const fs = F("foo");
// 调用逻辑的代码可以保持不变
h(f(fs).map((n) => Boolean(n)));
// 或者(注意调用 map 方法的对象不同)
h(f(fs.map((n) => Boolean(n))));
或者以pipe的形式,如下:
function app(s: string): boolean {
return pipe(F(s), f, h, (functor) => functor.map((n) => Boolean(n)));
}
后者相较于前者,它的优点在于引用透明。引用透明的含义指,任意函数,或者任意代码段,如果它可以被它的计算结果直接替代,仍然不影响任何调用它的程序,这里的n => Boolean(n)是纯函数,因此它是引用透明的,因此我可以毫无顾忌的把它换成其他实现逻辑,如n => !!n,只要它们是等价的。
而前者的实现中,由于m的逻辑是以一个中间件函数,或者侵入式地出现在带代码块中,在简单的情况下,对于m的实现细节可以做到了如指掌,但如果是复杂情况就不好说了,比如:
app的代码太过老旧,对其中的实现细节已经记不清了app的模块级别是 library 级别,更改代码的影响范围过大app缺少源码,如第三方模块
因此,使用 Functor 的写法,最大的优势就是做到了解耦,同时也保持了函数间的引用透明,更像是基于约定而编码,这也是函数式编程的代码具有非常好的语义的原因,这就好比你把钱存在银行,你很少会担心银行是否会偷偷把你的钱花掉,但如果你把钱保存在你的朋友手中呢?答案是显然的,这就是约定的强大之处,而函数式编程中的约定正是范畴论这个强大数学工具赋予的。
JS 中的 Functor
也许你可能不知道 Functor 的概念,但是你大概率已经在使用 Functor 了,因为 js 中的数组就是天生的 Functor,我们可以通过验证它是否具有范畴论中关于 Functor 要具备的两个属性来验证:
[identity('foo')]和identity(['foo'])等价[1].map(n => n * 2).map(n => n + 1)和[1].map(n => n * 2 + 1)等价
因此 Array 是 Functor。
那么 Promise 呢?同样来验证一下:
Promise.resolve(identity('foo'))和identity(Promise.resolve('foo'))等价Promise.resolve(1).then(n => n * 2).then(n => n + 1)和Promise.resolve(1).then(n => n * 2 + 1)等价
因此 Promise 也是 Functor。
如果我们要自己实现一个 Functor 呢?比如对于identity这个方法,实际上它本身就可以实现成一个 Functor,如下:
const Identity = (value) => ({
map: (fn) => Identity(fn(value)),
});
验证它是否满足 Functor 所具有的属性:
const foo = Identity("foo");
((x) => x)(foo); // Identity { 'foo' }
foo.map((x) => x); // Identity { 'foo' }
const two = Identity(2);
const f = (n) => n + 1;
const g = (n) => n * 2;
const r1 = u.map((x) => f(g(x))); // Identity { 5 }
const r2 = u.map(g).map(f); // Identity { 5 }
Functor 与 Type Class
Type Class 是函数式编程中一种非常重要的概念,它类似于面向对象编程中的接口(interface)。Type Class 定义了一个类型所需要实现的一组方法的接口,这些方法可以被任何实现该接口的类型所共用。Type Class 的用途是为了实现多态(polymorphism),在函数式编程中,多态的实现是通过对参数类型的抽象来实现的,Type Class 是一种描述这种抽象的方式。
Functor 本身就是一种 Type Class,它所描述的逻辑是映射,因此它有时候也被称作 Mappable,所以,它的 Type Class 是:
export interface Functor<A> {
readonly map: (fa: Functor<A>, f: (a: A) => B) => Functor<B>;
}
只有一个函数的参数实现了map方法,那么在函数式中,即可称该参数实现了MappableType Class。
实现一个 Type Class 往往非常简单,只需要实现它所要求的那个方法就行(如map),如果将 Type Class 当做一个函数的参数类型和返回值类型,又能够将任意的函数进行组合。因此,使用 Type Class 模式来实现多态,可以赋予代码强大的可组合性。
同时,一个参数类型可实现的 Type Class 并不是唯一的,它可以同时实现若干 Type Class,比如:
- 实现
map方法的 Type Class 是Functor - 再实现
ap方法则变成Apply - 再实现
of方法则变成Applicative - 再实现
chain或flatMap方法则变成Monad - …
这里对于上面所列举的 Type Class 就不展开说了,这里简单了解下函数式编程中,可组合性的强大之处即可。
这里我想提一下 Rxjs,如果你对它比较熟悉的话,应该会知道 Observable 这个概念,实际上从根上讲,Observable 就是一种 Type Class 的实现,这也是 Rxjs 可以被称作是一个基于函数式理念设计的响应式异步编程解决方案的原因。
实用的 Type Class
这里直接列举一些比较实用的 Type Class,文档源自 fp-ts,每个链接中都包含该 Type Class 的职能描述和代码示例。在之后的文章中,会针对每种 Type Class 提供一些具有实践意义的例子,以及它们怎样与前端开发结合,提升代码的可维护性、可扩展性和健壮性。